Dans le but de familiariser les élèves dès le plus jeune âge aux formations scientifiques, la Direction des Services Départementaux de l’Education Nationale de la Loire a créé les « Pôles scientifiques d’excellence » ayant pour objectifs : (i) engager les Etablissements dans une démarche de questionnement et de recherche , (ii) collaborer avec les laboratoires de recherche. Concrètement, à partir d’une question ou d’un matériau de recherche, posée ou apporté par le scientifique, la classe devra dépasser le défi scientifique pour entrer dans le raisonnement scientifique, s’engager dans une démarche de questionnements et de recherche. Dans le cas présent, le défi proposé aux élèves était de créer différentes numérations de leur choix et de restituer les savoirs acquis oralement et par voie d’affiches à leurs camarades et à un public d’adultes.

Cet article a été rédigé conjointement par Madame M. Frossard (Ecole Primaire Publique de la Cottencière St-Etienne, classe de CM2) et Monsieur J. Bourgois (Ecole des Mines de St-Etienne).

Dans un premier temps, il a été présenté aux élèves l’histoire de la numération, des hommes préhistoriques avec des entailles sur des os aux Mésopotamiens avec les calculis jusqu’à notre numération indo-arabe : au cours de ce grand voyage dans l’espace et dans le temps, ils ont étudié un peu d’histoire et un peu de géographie (les mathématiques menant à tout !). Puis les élèves se sont familiarisés avec les différents types de numération (additive, positionnelle ou mixte), incluant la notion de base en prenant pour exemple la base décimale. Une numération additive et décimale leur a été proposée (numération de l’Egypte antique) ainsi qu’une numération utilisant la base 4 (la numération des Shadoks). A la suite de cela, un défi leur a été donné : créer des numérations du type de leur choix pouvant être utilisées pour effectuer des calculs mathématiques. Les élèves ont formé eux-mêmes et par affinité 4 groupes de travail et voici leurs résultats.

La numération « naturelle » :

Il s’agit d’une numération additive décimale dont les symboles sont empruntés à la nature : une fleur, un arbre, un lac, une rose, un escargot, un oiseau ou un puits. Ces symboles ont respectivement pour valeur dans notre système : 1 – 10 – 100 – 1000 – 10000 – 100000 - 1000000.

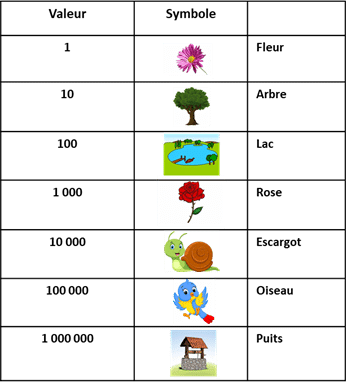
Le groupe d’élèves a présenté cette numération à la classe et a demandé à leurs camarades d’écrire différents nombres à l’aide de ces symboles, ce qui n’a pas posé de problème.

Puis, différents exercices ont été proposés : opérations et problèmes mathématiques (ces exercices ont été créés par les élèves sans intervention d’un adulte).

Faire des additions :

                    =?

                   =?

Faire des soustractions :

                 =?

                =?

Résoudre des problèmes :

Les solutions se trouvent en fin d’article.

La numération « catastrophe » :

Là encore, c’est une numération additive décimale, les symboles sont empruntés aux catastrophes naturelles : séisme, cyclone, volcan, incendie, avalanche et tsunami qui ont pour valeur : 1 - 10 - 100 - 1000 - 10000 - 100000 dans notre système.

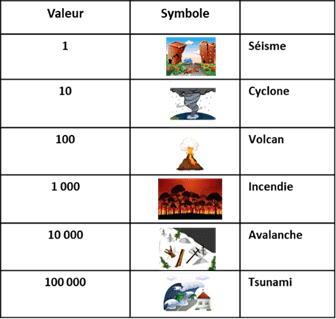
Une nouvelle fois, il n’y a pas eu de difficulté pour écrire différents nombres proposés par le groupe en utilisant ces symboles.

Exercices proposés par les élèves du groupe :

Additions :

                              =?

                           =?

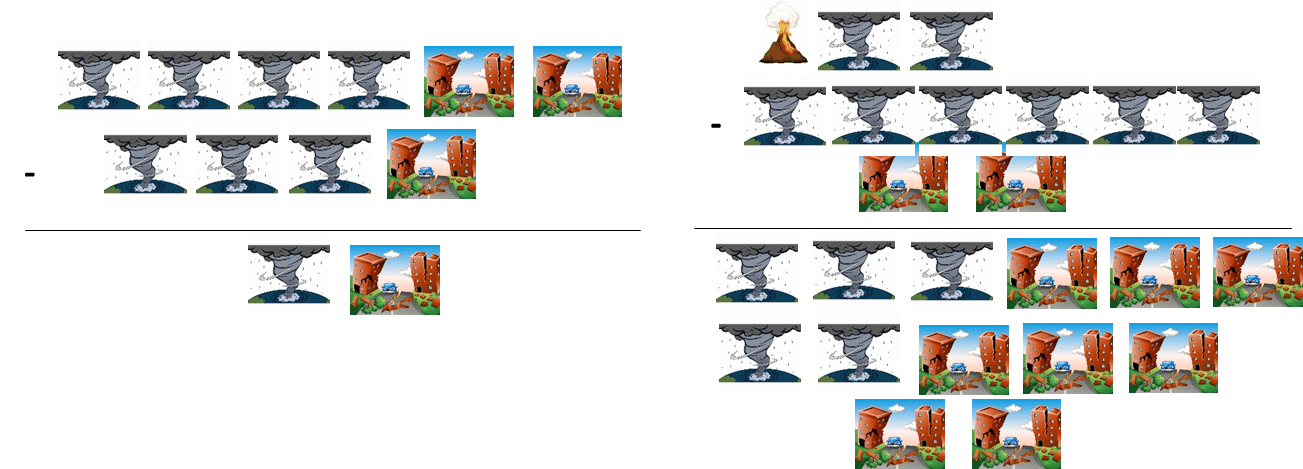
Soustractions :

                           =?

                           =?

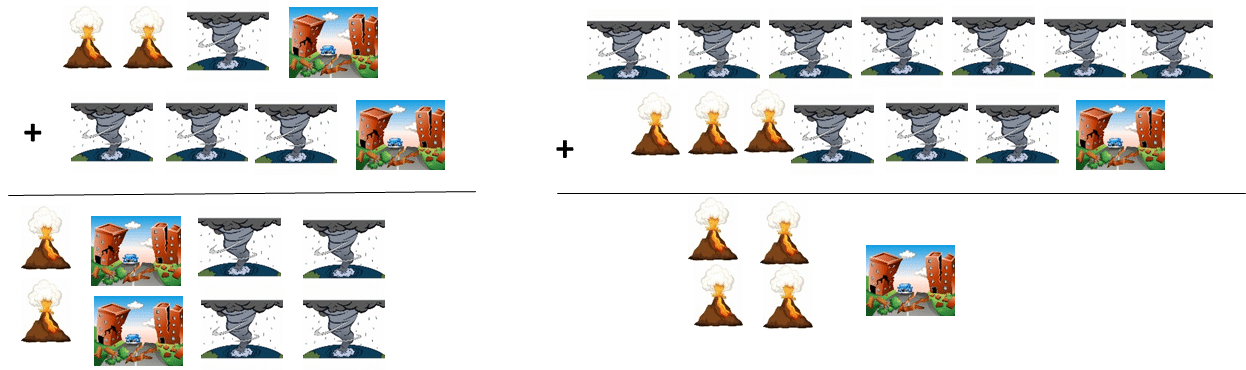
Problèmes mathématiques :

Les solutions se trouvent en fin d’article.

Conclusion : les élèves ont bien assimilé l’utilisation d’une base additive décimale.

Les deux autres groupes d’élèves ont choisi d’utiliser des numérations positionnelles autres que décimale.

La numération « OIVAE » :

Ce groupe a décidé d’utiliser la base 5 (nous avons cinq doigts sur une main). Ce système quinaire a été utilisé en Afrique jusqu’au XXème siècle et partiellement dans les notations romaines et mayas.

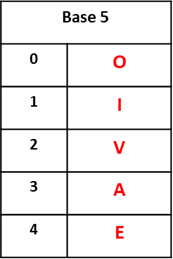
Cinq symboles sont utilisés, les lettres O, I, V, A et E. Pourquoi ces lettres ? leur graphie utilise 0, 1, 2, 3 ou 4 traits.

Cette fois, l’écriture de différents nombres proposés par le groupe en utilisant ces symboles a été un peu plus laborieuse mais néanmoins réussie.

Comme la numération OIVAE est positionnelle, les élèves du groupe ont pu écrire les tables d’addition et de multiplication utilisant cette notation afin de pouvoir résoudre quelques problèmes mathématiques :

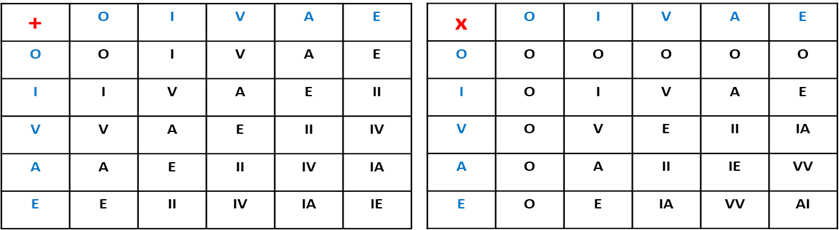
Exercices proposés par ce groupe d’élèves :

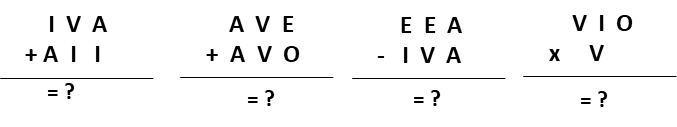
Les solutions se trouvent en fin d’article.

La numération « géométrique » :

Le second groupe a utilisé la base 6. Pourquoi la base 6, mystère ! mais sans le savoir les élèves ont utilisé le système sénaire qui est utilisé dans des langues de Papouasie-Nouvelle-Guinée et plus proche de nous dans les dés à jouer.

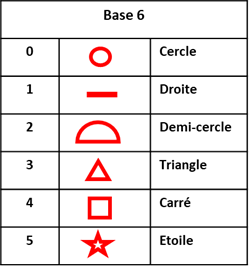
Six symboles sont utilisés : le cercle, la droite, le demi-cercle, le triangle, le carré et l’étoile à 5 branches. La valeur de ces symboles est égale au nombre de lignes utilisées pour les dessiner (un peu moins vrai pour le cercle et pour l’étoile !).

Là encore, l’écriture de différents nombres proposés par le groupe en utilisant ces symboles a été un peu plus laborieuse que celle des numérations additives mais néanmoins réussie dans l’ensemble. La base 6 est un peu plus compliquée que la base 5 puisqu’une main ne comporte pas 6 doigts !

Comme la numération géométrique est positionnelle, les élèves ont écrit les tables d’addition et de multiplication utilisant cette notation afin de pouvoir résoudre quelques problèmes mathématiques :

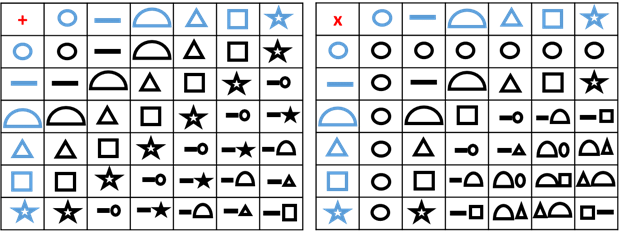
Exercices proposés par ce groupe d’élèves :

Les solutions se trouvent en fin d’article.

Conclusion générale

Les auteurs remercient les élèves de la classe d’avoir relevé, avec enthousiasme, le défi proposé. Ce dernier leur a permis d’appréhender les calculs avec une autre méthode que celle qu’ils ont l’habitude d’utiliser. De plus, ils ont utilisé d’eux-mêmes les bases de toute recherche scientifique : poser le problème, discuter des diverses solutions possibles, retenir la meilleure à la suite d’essais-erreurs puis restituer les résultats acquis. Ils ont appris à travailler ensemble et à prendre des décisions en groupe en se remettant en question, en admettant leurs erreurs et à proposer des solutions pour les corriger. Le moment de restitution a été un moment très émouvant pour les auditeurs : voir les élèves expliquer, avec une certaine fierté et une grande motivation, à leurs camarades des notions nouvelles (et pas toujours simples) en s’appuyant sur des affiches créées par eux-mêmes, leur poser des problèmes … toutes choses qu’ils n’ont pas toujours l’habitude de faire.

Au départ, les auteurs de ces quelques lignes avaient la crainte d’entendre :

• « J’aime pas les maths »
• « Pour les tables de multiplication et d’addition, y-a des calculatrices »
• « Savoir compter comme les Egyptiens, à quoi ça sert ? »

Mais ils n’ont pas eu besoin de motiver les élèves qui se sont immédiatement pris au jeu de la création scientifique. Et en plus, compter comme les Shadoks (GA-BU-ZO-MEU), ça s’est amusant !

Au cours de la restitution, les élèves étaient tous attentifs, peut-être étaient-ils intimidés mais sans doute étaient-ils fiers de leur travail. Un bon moment pour les élèves et pour nous.

Solutions des exercices :

Numération « naturelle » :

Numération « catastrophe »

Numération « OIVAE »

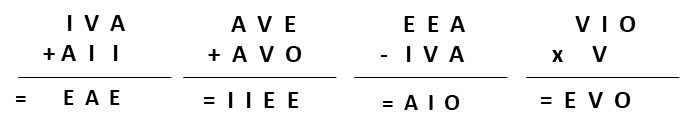
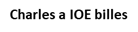
Numération « géométrique »