Nous avons tous été fascinés par l’Egypte antique : les pyramides, le sphinx de Gizeh, les temples … A la lecture des nombreux papyrus retrouvés dans diverses tombes, nous savons que les Egyptiens ont été précurseurs dans de nombreux domaines : la médecine avec la chirurgie, le calendrier (année solaire de 365 jours, journée de 24 heures), la cosmétique (maquillage, perruque, brosse à dents, rasoir …), les bibliothèques (la plus célèbre : celle d’Alexandrie), le tissage, les papyrus sur lesquels ils notaient leurs savoirs, la fabrication du verre, l’architecture, les mathématiques (arithmétique, géométrie).

Si cette civilisation connaissait les mathématiques, c’est que les Egyptiens savaient compter. Comment faisaient-ils ? Comment écrivaient-ils les nombres ? Comment résolvaient-ils les problèmes mathématiques ? C’est l’objet de ce présent article.

Les parties I et II de ce dossier ont été consacrées à présenter respectivement les origines des nombres et les différents systèmes de numération.

Partie I : les origines

Partie II : les systèmes de numération

La numération additive chez les Egyptiens :

Les Egyptiens utilisaient un système de numération à base décimal dans lequel le zéro n’existait pas. Chaque puissance de 10 était représentée par un hiéroglyphe.

Avec ces 7 hiéroglyphes, les Egyptiens pouvaient compter jusqu’à 9 999 999. S’agissant d’un système additif, les symboles sont répétés autant de fois que nécessaire (sans dépasser 9) pour représenter un nombre. La place du hiéroglyphe n’a aucune importance dans l’écriture du nombre, le scribe écrivait ces symboles afin de rendre l’ensemble harmonieux.

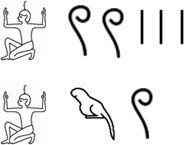
Exemple : 2 100 303 = 2x1000000 + 1x100000 + 3x100 +3x1

Ce système, bien que simple, a cependant un inconvénient car si l’on souhaite écrire 9999, il faut 36 symboles (9 fleurs de lotus+9 rouleaux de papyrus+9 anses de panier+9 bâtons) !

Les fractions égyptiennes :

Un peu d’histoire : Horus (dieu à tête de faucon) fils d’Isis et d’Osiris, fit la guerre à son oncle Seth pour venger l’assassinat de son père. Au cours d’un des nombreux combats, Seth lui arracha l’œil gauche, le découpa en six morceaux qu’il jeta dans le Nil. A l’aide d’un filet, Thot (dieu des scribes) repêcha les morceaux mais en oublia un. Il réussit néanmoins à reconstituer l’œil en ajoutant une particule divine et le rendit à Horus afin qu’il puisse voir au-delà du visible.

L’œil d’Horus a été représenté sur des sarcophages ou des pectoraux afin de protéger contre le mauvais sort, il a été également peint sur la proue des bateaux afin de tenir le bon cap.

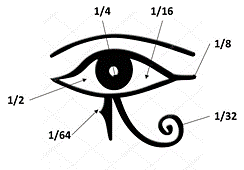
En 1911, l’égyptologue Georg Möller pensa que les parties de l’oeil d’Horus représentaient les fractions unitaires : 1/2 (conjonctive) 1/4 (pupille) 1/8 (sourcil) 1/16 (conjonctive) 1/32 (une larme) 1/64 (tâche du faucon). Si l’on fait la somme de six valeurs le résultat est 63/64, le 1/64^ième manquant pourrait être l’élément magique ajouté par Thot pour que l’œil fonctionne parfaitement.

Pour cette raison, en dehors des entiers les Égyptiens ne concevaient que les fractions unitaires (1/2 1/3 1/4 ...) sauf 2/3 et 3/4. Ces fractions sont représentées par des symboles : une bouche surmontant le dénominateur.

Il existait des symboles spéciaux pour les fractions les plus courantes :

1/2

2/3

3/4

Les factions non unitaires étaient décomposées en fractions unitaires en utilisant des tables. La table de 2 est ainsi :

2/5 = 1/3 + 1/15

2/7 = 1/4 + 1/28

…

Les opérations arithmétiques égyptiennes

L’étude de papyrus, dont le plus célèbre est le papyrus de Rhind, a permis d’expliquer les mathématiques égyptiennes.

Addition : cette opération est simple avec le système additif, il suffit de regrouper les symboles des deux nombres à additionner et de les compter (si le résultat dépasse 10 pour un symbole donné, le scribe remplaçait 10 symboles identiques par le symbole immédiatement supérieur).

Exemple : 2033 + 20081 = 22104

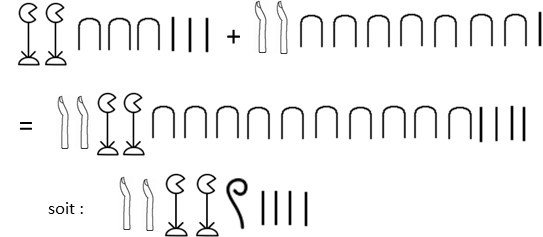
Soustraction : la technique inverse est utilisée, il suffit d’enlever au premier nombre les symboles du second

Exemple : 22105 - 20071 = 2034

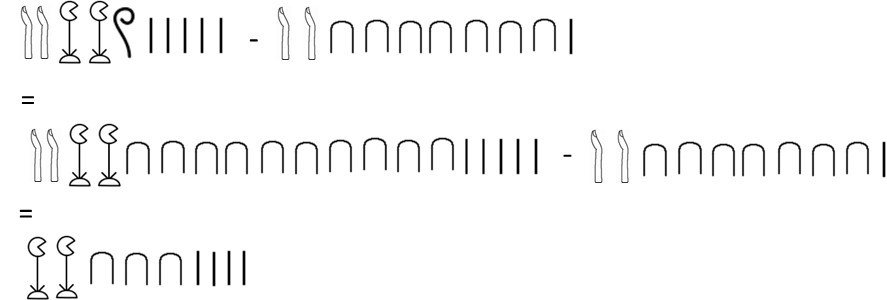
Multiplication : les tables de multiplication n’existant pas, les Egyptiens ont inventé une méthode ne demandant qu’à multiplier par deux (ce qui revient à une addition) puis à faire des additions. La technique consiste à décomposer le plus petit nombre en une addition de puissances de 2 et à créer une table des multiples du second nombre (second nombre x puissance de 2).

La technique de la multiplication égyptienne est présentée en fin d'article pour les lecteurs intéressés.

Division : la technique de la division égyptienne repose sur le même principe que celui de la multiplication.

La technique de la division égyptienne est présentée en fin d'article pour les lecteurs intéressés.

Géométrie : Si les Egyptiens ont pu bâtir de si grandioses monuments, c’est qu’ils avaient des connaissances reconnues en géométrie. En effet, ils savaient calculer des surfaces (rectangle, triangle, trapèze, disque, sphère, …) et des volumes (cube, pyramide, cylindre, cône, …)

Le résultat le plus remarquable est la connaissance d’une constante, qui deviendra par la suite le nombre PI, utilisée dans le calcul de la surface d’un disque.

Énoncé du problème R50 du papyrus Rhind :

« Exemple de calcul d'un champ rond de neuf khet. De combien est la surface du champ ? Soustrais son neuvième qui est un. Il reste huit. Multiplie huit par huit. Cela fait soixante-quatre. Ceci est la surface du champ, à savoir soixante-quatre setjat. Fais comme suit : »

[1 khet=52,6 m environ, 1 setjat=2771 m² environ]

Ce qui veut dire : soit d (ici d=9 khet) le diamètre du champ, on en soustrait 1/9, il reste 8/9 d. On multiplie cette valeur par elle-même, ce qui fait 64/81d² qui est la surface du champ = 64 setjat.

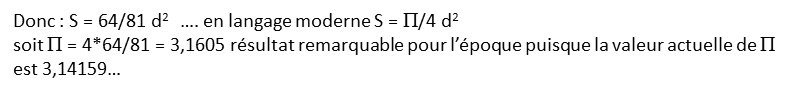
Résolution d’équations mathématiques : Les scribes égyptiens savaient résoudre les équations de premier et du second degré, calculer les racines carrées et connaissaient les suites arithmétiques et géométriques.

Légende ou réalité ? Les Egyptiens devaient reconstituer les champs rectangulaires détruits par les crues du Nil. 

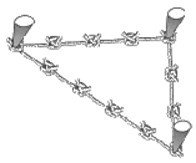
Mais comment obtenir des angles droits ? Ils auraient probablement utilisé la célèbre corde à 13 nœuds (1 nœud à chaque extrémité, soit 12 intervalles égaux). Avec cette corde, outre les triangles rectangles, il est également possible  de dessiner des triangles isocèles, des carrés, des rectangles, des losanges, des trapèzes, ...

Les Egyptiens auraient-ils inventé le théorème de Pythagore ? ou cela ne serait-il qu'un résultat empirique ?

Et avec toutes ces connaissances, les Egyptiens ont su bâtir des œuvres ‘pharaoniques’ comme par exemples les pyramides, les temples, le sphinx …

Remerciements : L'auteur remercie Aourell LANFREY (médiatrice scientifique, La Rotonde, Ecole des Mines de Saint-Etienne) de sa participation à l'élaboration de cet article. 

Pour en savoir plus sur la technique de la multiplication utilisée en Egypte antique :

La technique consiste à décomposer le plus petit nombre en une addition de puissances de 2 et à créer une table des multiples du second nombre (second nombre x puissance de 2).

Soit par exemple 14x23 en représentation indo-arabe pour plus de simplicité :

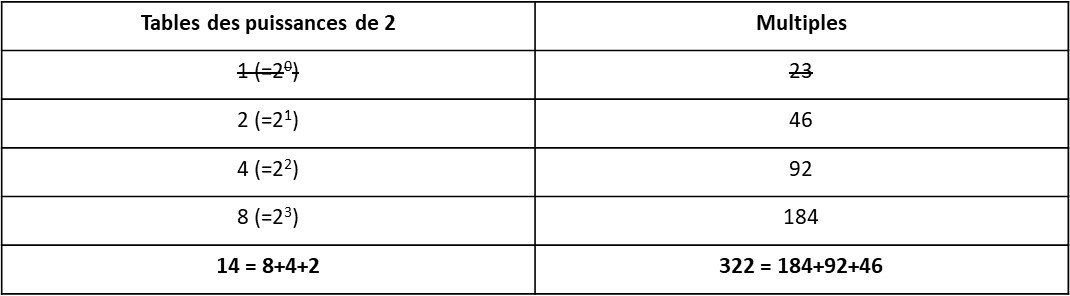
Le multiplicateur 14 est égal à la somme des puissances de 2 suivante 8+4+2, la puissance de 2 restante est supprimée (ici 1). Il convient également de supprimer les multiples de la seconde colonne correspondants (ici 23). Le résultat de la multiplication est égal à la somme des multiples restant : 23x14 = 322 = 184+92+46

Cette même multiplication dans le système égyptien :

Pour en savoir plus sur la technique de la division utilisée en Egypte antique :

Une première colonne regroupe les puissances de 2 et une seconde les valeurs du diviseur multipliées par les puissances de 2 de la première colonne jusqu’à atteindre la plus grande valeur inférieure au dividende. Ensuite, il convient de recomposer le dividende par une somme de valeurs de la seconde colonne et le résultat de la division est la somme des puissances de 2 correspondantes. Par exemple : 125/5 (=25)

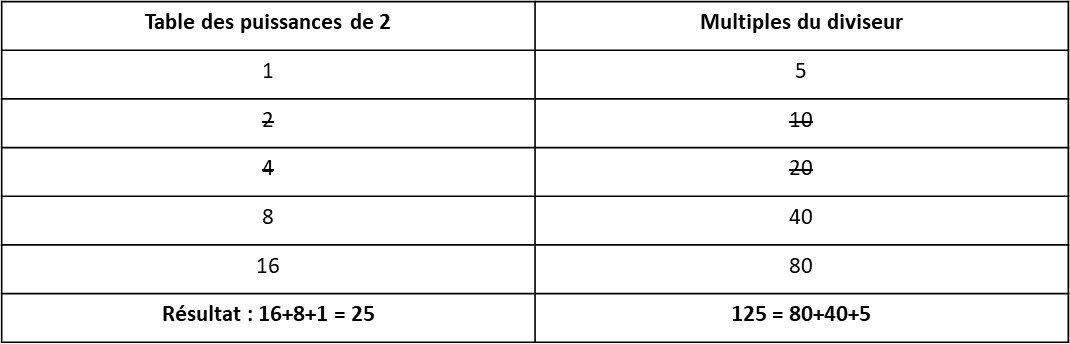
Le même principe est utilisé pour les divisions dont le résultat est un nombre fractionnaire ou pour les divisions dont l’un des deux opérateurs est fractionnaire.

Par exemple : 26/5 (=5,2)

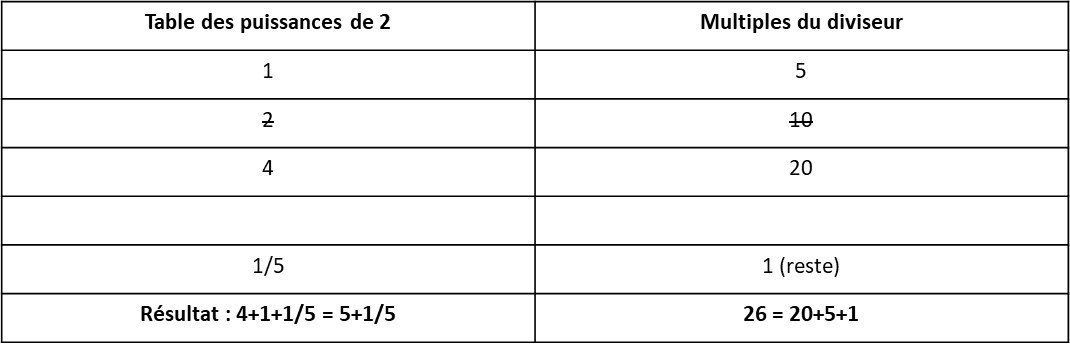
La somme des multiples est égale à 25, il faut encore ajouter 1 pour obtenir le dividende 26, 1 est le cinquième du diviseur : le résultat de la division est donc : 5+1/5 soit 5,2.

Si le diviseur est fractionnaire : soit 16/3,2 (=5)

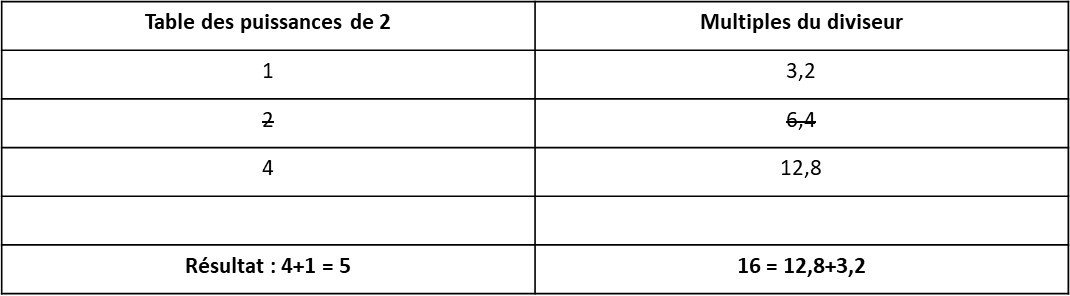
Le résultat est 5.

Pour en savoir plus sur ces types de division : voir le site suivant

Technique de la division dans l'Égypte antique — Wikipédia (wikipedia.org)