Il était une fois...la numération. partie VI : les numérations mixte et positionnelle chinoises

Publié par Jacques Bourgois, le 2 juin 2022 3.6k

Les Chinois antiques ont toujours été en avance sur les autres civilisations pour la création de nouvelles inventions qui ont parcourues le monde et qui sont toujours utilisées de nos jours : le papier, la soie, la porcelaine … dans le domaine technique : le fer, la boussole, le forage profond ; dans le domaine de la médecine : l’acuponcture …

Pour les Chinois, les mathématiques étaient indispensables pour gouverner l’Empire (calcul des revenus, perception des impôts, partage des terres …) mais également dans la vie quotidienne. L’étude des calculs mathématiques remontent au VI/V^ème siècle av.J.C. Quel était leur type de numération ?

Les premiers vestiges de représentation des nombres datent d’environ 4000 ans. Des carapaces de tortue servant à des cérémonies religieuses ont été découvertes en 1899 dans la province du Henan, y étaient gravées des informations numériques indiquant le nombre d’hommes perdus à la guerre, de prisonniers ennemis, d’animaux tués à la chasse …

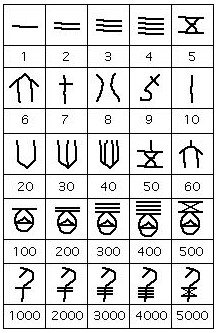
Ce premier système de numération fait appel à 9 symboles fondamentaux (1 à 9) et aux 3 premières puissances de 10 (10, 100, 1000). Les autres symboles de la figure précédentes sont construits à partir des symboles précédents : par exemple 50 est écrit à partir des symboles 5 et 10. Cette numération décimale n’est basée que sur des multiplications et des additions (c’est pour cela qu’on la désigne comme mixte), la valeur du chiffre ne dépend pas de sa position dans le nombre.

Nature multiplicative : 300 est représenté par les symbole 3 et 100 placés d’une certaine façon l’un par rapport à l’autre, 5000 est représenté par les symbole 5 et 1000.

Nature additive : 2156 est représenté par le symbole 2000 suivi du symbole 100, suivi du symbole 50 puis du symbole 6.

Exemple : 4359 = 4000 + 300 +50 + 9

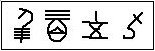
Puis au cours du temps, les écritures ont évolué pour devenir les 13 symboles suivants : les symboles présentés ci-dessous sont les symboles modernes qui ne diffèrent pas énormément des symboles anciens datant d’il y a environ 2500 ans.

Le système décimal a ses origines en Chine, il date du XIVème siècle av.J.C. (dynastie Shang) alors que les premières traces de ce système en Europe apparaissent vers l’an 1000 après J.C. dans un manuscrit espagnol. Cette numération décimale utilise 9 symboles pour les unités, et 4 pour les puissances de dix (10 ;100 ;1000 ;10 000).

Un nombre est écrit en une suite de caractères et est décomposé en dizaines de milliers (et non en milliers comme dans le monde occidental) : le nombre occidental 716 323 180 000, en utilisant la numération chinoise s’écrit 7163 2318 0000.

Pour écrire un nombre, les Chinois énumèrent le nombre de dizaines de milliers, le nombres de milliers, le nombres de centaines, le nombre de dizaines et enfin le nombre d’unités.

Ainsi :

147 est écrit :

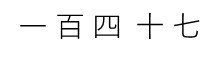
soit 1x100 + 4x10 + 7

2022 est écrit :

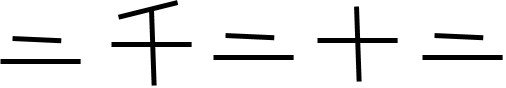
soit 2x1000 + 2x10 + 2

7236 3281 0000 est écrit :

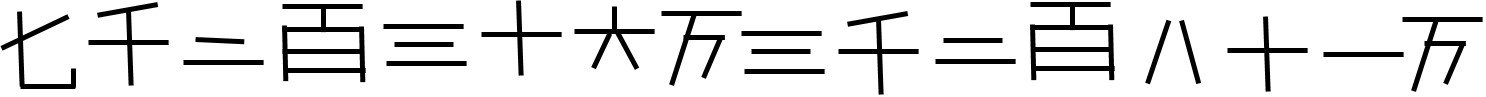
soit [(7x1000+2x100+3x10+6)x10000 + (3x1000+2x100+8x10+1)] x 10000

Notons que ce système, n’étant pas purement positionnelle, n’a pas besoin d’un symbole représentant le zéro.

Les symboles précédents ne servent qu’à écrire des nombres, ils ne pouvaient être utilisés pour effectuer des calculs. Il suffisait de peu de chose pour que le système chinois ancien devienne positionnel et soit ainsi apte à faire des calculs au même titre que notre système indo-arabe : avoir un symbole pour le zéro et savoir que la valeur du chiffre dépend de sa position dans le nombre. Notons que cette numération mixte est également la nôtre à l’oral : 234 se prononce deux cent trente-quatre (soit 200 + 30 + 4).

Vers l’an 700 av.J.C est apparue la numération dite des ‘baguettes’ plus propice aux calculs, elle va exister jusque vers 1400 après JC. Elle est décimale avec 9 symboles. Ce système est positionnel : étant décimal avec 9 symboles c’est impossible ! il faut ajouter quelque chose qui doit être le zéro, ce sera un espace blanc. Ces baguettes ont d’abord été en bambou puis en bois, métal, ivoire ou jade.

Les 9 symboles utilisés sont les suivants et sont disposés sur un échiquier appelé ‘suanpan’ :

Exemples de nombres :

16 :

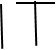
267 :

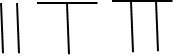
Mais il y a un problème de taille : comment différencier 2 de 11 ou de 110 ou encore de 1100 ? si on ajoute un espace entre les deux barres verticales, cela fait 101.

II = 2

II = 11

II = 110 ou 1100

I I = 101

Le problème a rapidement été résolu en différenciant les symboles selon les puissances de 10 avec deux séries de symboles : barres verticales pour les puissances de 10 paires (unités, centaines, dizaines de milliers …), barres horizontales pour les puissances de 10 impaires (dizaines, milliers …). Sunzi suan jing (fin 3^ième siècle) écrit dans ‘Le classique mathématique’ : « Les unités sont verticales, les dizaines sont horizontales, les centaines sont debout, les milliers sont couchées ; mille et dix sont pareils, dix-mille et cent se ressemblent ».

Ainsi, 1235 s’écrit :

308 s’écrit :

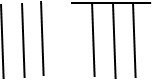
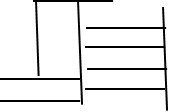
Mais tout n’est pas si simple, car dans les manuscrits il est possible de trouver les nombres écrits sous forme de monogrammes : par exemple 7641 écrit normalement et sous forme de monogramme

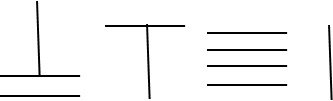
Le livre de mathématiques le plus célèbre est le ‘Chiu-Chang Suan-shu’ (L’Art mathématique en neuf sections) datant probablement du premier siècle. Il y ait fait mention :

Des additions et des soustractions de fractions et des pourcentages
De la règle de trois pour les distributions proportionnelles
Des racines carrées et cubiques
Des volumes des solides
Des résolutions de systèmes d’équations à deux inconnues
Des problèmes liés au triangle rectangle
Du nombre PI en considérant un polygone régulier à 172 côtés (PI=3,14159)

Au II^ème siècle av.J.C. les Chinois utilisaient déjà les nombres négatifs : les nombres positifs étaient représentés par des baguettes rouges et les nombres négatifs par des baguettes noires. Lors des échanges commerciaux, le montant vendu était positif (on recevait de l’argent), le montant dépensé était négatif (on dépensait de l’argent). Si les Chinois utilisaient les nombres négatifs, ils refusaient cependant d’admettre qu’un nombre négatif puisse être solution d’une équation mathématique. Lorsque les nombres négatifs devaient être écrits, une baguette oblique était placée sur le chiffre non nul le plus à droite du nombre : - 162

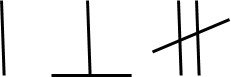
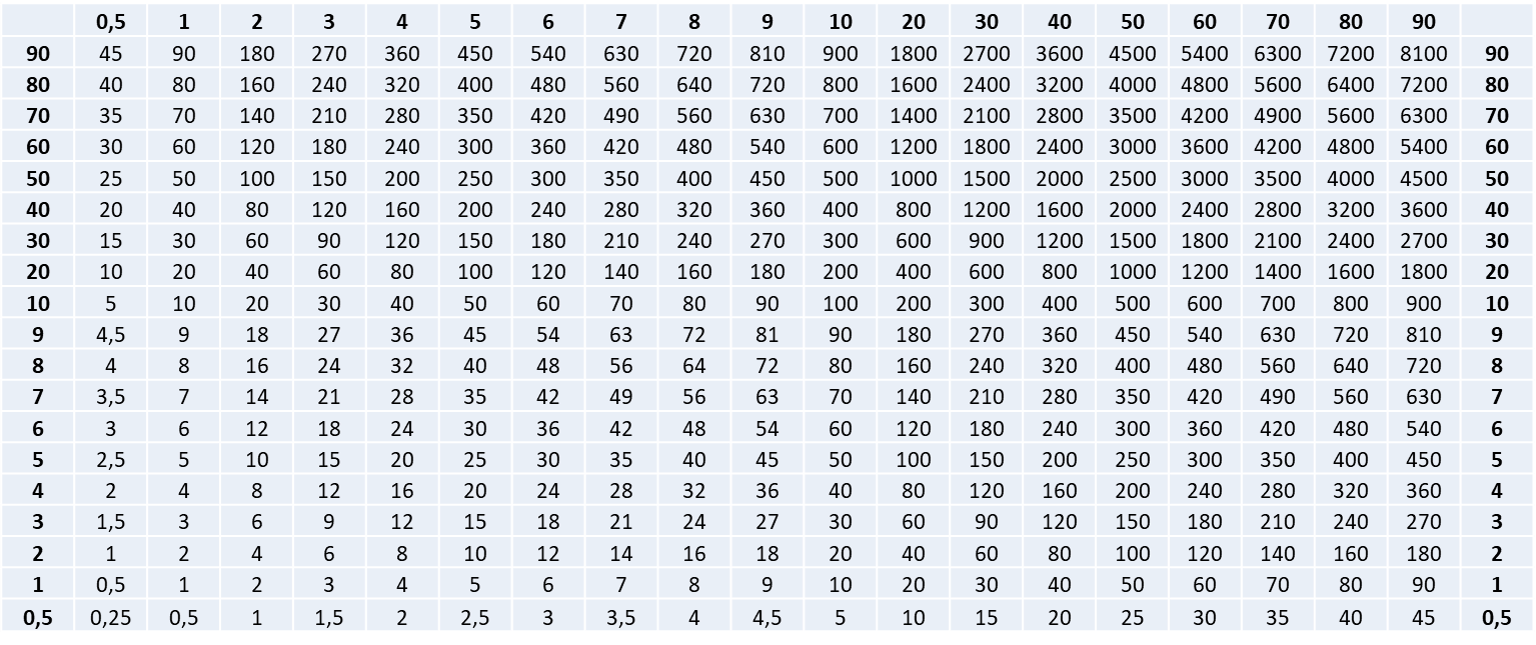
Les additions et les soustractions se faisaient pratiquement selon la même méthode que celle que nous utilisons actuellement (voir en fin d’article). Pour les multiplications, la méthode chinoise était également proche de la nôtre (voir en fin d’article) en utilisant les tables de multiplication (305 av.J.C., tables écrites sur des feuilles de bambou et retrouvées lors de fouilles archéologiques).

Table multiplication chinoise 305 avJC (bandelettes en bambou) : dans les 1^ère ligne et les colonnes extrêmes y figurent 19 nombres : 0,5 et les entiers jusqu’à 9, les multiples de 10 jusqu’à 90; dans les autres cellules la valeur de la multiplication.

Le boulier chinois ou ‘zhu suan’ (zhu=perle, suan=compter) également connu sous le nom de suanpan est un abaque servant à compter. Mentionné dès de IIème siècle en concurrence avec le calcul à baguettes, il est utilisé depuis plus de 8 siècles. Il est constitué de tiges sur lesquelles coulissent des billes.

Sur chaque tige se trouvent 5 billes représentant une unité et 2 billes représentant 5 unités. En déplaçant les billes, il est possible d’additionner, de soustraire, de multiplier, de diviser, d’extraire des racines, de calculer des puissances … La rapidité des calculs fait que ce boulier a été nommé le plus vieil ‘ordinateur’ du monde. L’utilisation du boulier chinois est expliqué sur le site suivant :

https://saidaguezoui.fr/assets... · Fichier PDF

Les fractions : dès le deuxième siècle av.J.C., les Chinois utilisaient les fractions alors qu’en Europe elles ne sont apparues qu’au XVème siècle. Ils savaient les réduire, les additionner, les soustraire, les multiplier. Les fractions étaient nommées comme suit : 2/3 |de volume| était nommé 2 des 3 parts |de volume| : on prend 2 parts |d’un volume| divisé en 3 parts. Dans les deux types de numération cités dans cet article, l’écriture est la suivante :

ce qui correspond à : 3 parts |de volume| partage 2 ... ce qui correspond à 2 de 3 part |de volume|

avec les baguettes, le numérateur est écrit au dessus du dénominateur : 2/3 par exemple

Les opérations mathématiques courantes utilisant des fractions étaient très proches de notre mode de calcul.

Les carrés magiques : le plus ancien carré magique connu à ce jour est le carré de Lo Shu (2200 av.J.C.), d'après la légende il aurait été lu par l'empereur YU sur la carapace d'une tortue sacrée le long de la rivière Lo. Ce carré d'ordre 3 (3 lignes et 3 colonnes) possède une constante égale à 15 : la somme des chiffres de chaque colonne, de chaque ligne et de chaque diagonale est égale à 15.

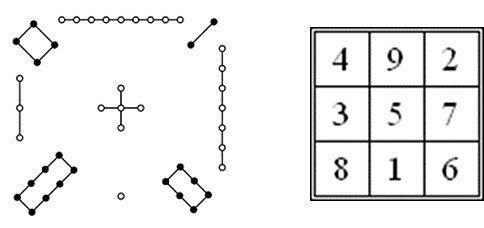
Par la suite, les carrés magiques ont été repris par les Grecs, Mésopotamiens, Arabes à des fins mathématiques. Dans de nombreuses civilisations d'Europe ou d'Asie ces carrés ont une connotation religieuse, astrologique ou alchimiste.

Pour en savoir plus :

Addition et soustraction chinoises

Ces opérations se font à partir des symboles les plus forts (de gauche à droite), les retenues étant immédiatement appliquées s’il y a lieu.

Addition : exemple 747+162. Les résultats intermédiaires s’écrivent sur la ligne supérieure

747

162

Etape 1 : 7+1=8, remplacer le 7 des centaines par 8, enlever le 1 de 162

847

Etape 2 : 6+4=10, remplacer le 4 des dizaines par 0 et le 8 des centaines par 9 puisque retenue de 1, enlever le 6 de 62

907

Etape 3 : 7+2=9, remplacer le 7 des unités par 9, enlever le 2 de 2

909

Etape 4 : lire le résultat 909

Soustraction : exemple 4235-782. Les résultats intermédiaires s’écrivent sur la ligne supérieure

4235

782

Etape 1 : 12-7=5, remplacer le 2 des centaines par 5 et le 4 des milliers par 3 (retenue de 1), enlever le 7 de 782

3535

Etape 2 : 13-8=5, remplacer le 3 des dizaines par 5 et le 5 des centaines par 4 (retenue de 1), enlever le 8 de 82

3455

Etape 3 : 5-2=3, remplacer le 5 des unités par 3, enlever le 2 de 2

3453

Etape 4 : lire le résultat 3453

Multiplication et division chinoises

Ces opérations nécessitent trois lignes. Sur la première est écrit le multiplicande ou le dividende, sur la seconde les résultats intermédiaires et sur la troisième le multiplicateur ou le diviseur

Multiplication : exemple 18x32. Les résultats intermédiaires s’écrivent sur une ligne séparée

Etape 1 : 3 dizaines de 32 fois 1 dizaine de 18 = 3 centaines d’unités

Etape 2 : 2 unités de 32 fois 1 dizaine de 18 = 2 dizaines d’unités. Faire la somme des centaines si nécessaire

Etape 3 : 3 dizaines de 32 fois 8 unités de 18 = 24 dizaines d’unités. Faire la somme de centaines et des dizaines si nécessaire

Etape 4 : 2 unités de 32 fois 8 unités de 18 = 16 unités. Faire la somme des centaines et des dizaines si nécessaire

576

Etape 5 : lire le résultat de la multiplication 576 sur la ligne ‘résultats intermédiaires’

Division : exemple 309/7

309

Etape 1 : si le nombre de centaines est supérieur au diviseur, diviser le nombre de centaines par le diviseur, si non diviser le nombre de dizaines par le diviseur (ici 30/7), écrire le résultat sur la ligne intermédiaire et retrancher le produit ‘résultat intermédiaire x diviseur’ du nombre de centaines utilisé (ici 30-28=2)

Etape 2 : répéter l’opération précédente

Etape 3 : lire le résultat 309/7 = 44+1/7

Remerciements : L'auteur remercie Aourell LANFREY (médiatrice scientifique, La Rotonde, Ecole des Mines de Saint-Etienne) de sa participation à l'élaboration de cet article.

Le calcul à baguettes – Neuf Chapitres Trois Quarts (wordpress.com)

LA NUMERATION CHINOISE (ac-orleans-tours.fr)

Histoires de multiplications (univ-amu.fr)

http://math.univ-lyon1.fr/irem...

https://mathschine.univ-lille....

https://chine.in/guide/numerat...

CHINE : Maths-rometus, Mathématiques chinoises, Civilisation mathématicienne, Histoire des maths, Maths, Mathématiques, Math, Jean-Luc Romet

Carré de Luo Shu — Wikipédia (wikipedia.org)

Les carrés magiques : Introduction - Canaux, Maths et Carrés magiques (canal-math.com)